
The current approach to learning math in Singapore primary schools is through the math model method. Under this approach, students are required to draw math models that illustrate the questions. For lower primary students, modeling might seem unnecessary but the skills being mastered will come in handy at upper primary level where problem sums becoming more challenging. To give your lower primary child a head start, this article will show you some techniques for math modeling.
1. Background on math model method
This methodology was created by a Singaporean teacher called Hector Chee. Due to its practicality, the method was soon taught in all schools, starting from Primary One. This new method presented a challenge to parents who might have been taught using algebra or other math methods. As a result, many could not help their children to develop the right math model techniques for the different kinds of math problem sums.
2. Main concepts in Singapore math model method
In the math model method, there are basically 2 concepts that form the foundation for all further iterations.
2.1 The part whole concept
In this concept, the child starts with understanding the relationship between parts. Once understood, they can represent these relationships using rectangular blocks to model math questions.
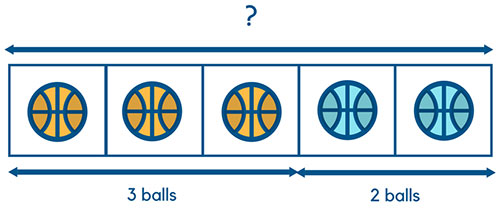
Let’s look at one example to better understand how the part whole concept works. In the image below, the child starts off learning how to add the individual balls to understand a simple addition question of 3 +2 =5. At this stage, it is important to use real images such as the balls to let the child connect the dots.
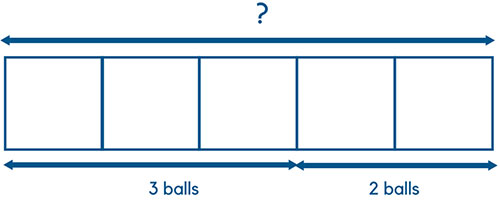
Once the child has understood the above, we can take out the balls and uses blocks as representations. Below is how the image can be drawn. Once the kid accepts the blocks as representations, he or she will be in a good position to understand further abstraction.
After the above, we can go one step further to visualize the question in even more abstract terms. Here, we don’t need the individual blocks. Instead, just a visual distinction between 3 and 2 is enough to represent the relationship between the blocks.
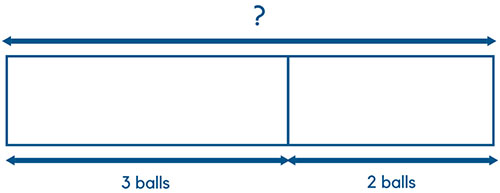
In summary, this technique uses the relationship of the parts to let children learn about the whole.
2.2 The change concept
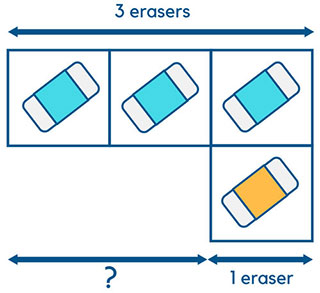
The change concept helps children to understand the concepts of adding and subtracting. Let’s take a look at an example of subtraction. In the example below, we are teaching a child how to subtract 1 from 3 i.e. 3-1=2. Again, we start off the math model by using realistic objects.
Once the child is similar with subtracting, we can proceed to using a more abstract representation. In this step, we replace the objects with blocks.
In the final step, replace the individual blocks with larger blocks. This sets the foundation of all future problems where a child can just use the bigger blocks to present items that can be added or subtracted.
This will help your child to see what is the change answer to the problem sum questions.
3. Applying math models to learning fractions, ratios and decimals
Now that you are familiar with the basic math models, I will show you how you can use them in solving different types of math problems.
3.1 Fractions
Fractions can be represented using the part whole concept. F0r the purpose of illustration, let’s solve the following problem sum on fractions.
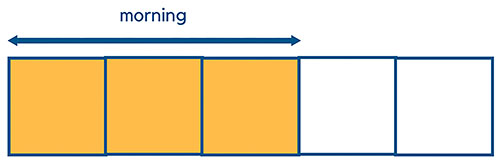
“Peter is selling pencils. He sold 3/5 of them in the morning and 1/4 of the remainder in the afternoon. If Peter sold 200 more pencils in the morning than in the afternoon, how many pencils did Peter have in the beginning?”
To solve this problem sum, we will use the part whole concept to draw the following math model. First, draw 5 equal blocks and shade 3 of them to represent 3/5.
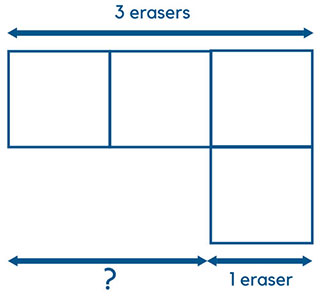
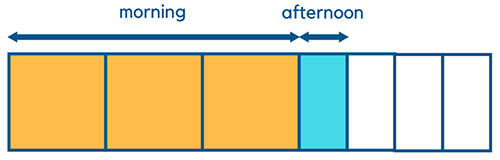
Next, divide the unshaded portion into 4 parts and shade one of them in a different color to show 1/4 of the remainder
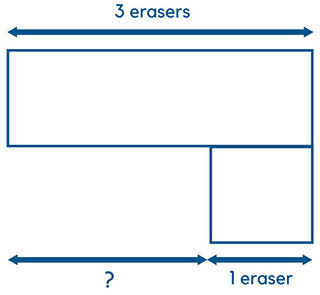
The third step is to make all boxes equal by cutting 1 red shaded box into 2 as shown below.
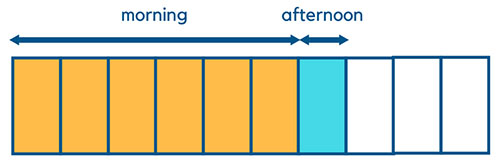
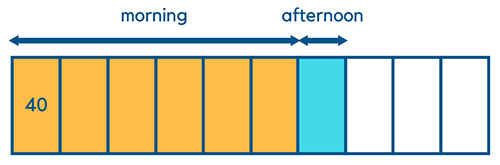
The fourth step is to calculate how many pencils does each box represents. The question says that there are 200 more pencils being sold in the morning. In this case, 200 is equal to 5 red boxes since there are 5 more shaded boxes in the morning. So, each box = 200/5 = 40.
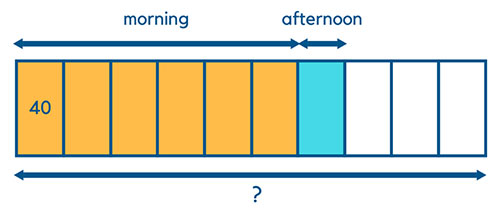
The final step is to calculate the total number of pencils. Since there are 10 boxes in total, the answer to the question is 40 * 10 = 400 pencils. The final math model will look like the below:
3.2 Ratios
For learning ratios, you can use either the part whole concept or the change concept. In the example here, we will use the change concept.
“The ratio of Amy and Karen’s money is 5:3. After Amy spent half of her money, she had $15 less than Karen. What was the total amount of money that both girls had in the beginning?”
The first step is to draw out the ratio.
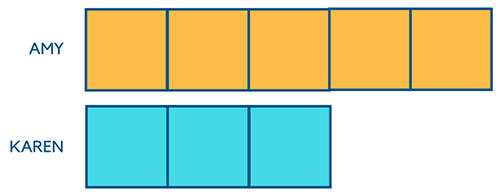
The next step is to draw out the diagram after Amy has spent half of her money.
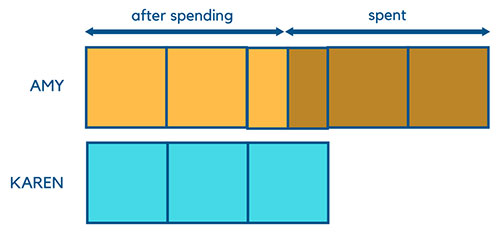
The third step is to shade out the block that represents the difference between Amy and Karen’s money.
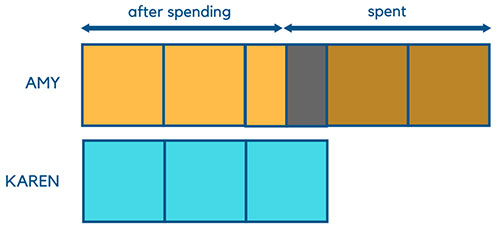
The question tells us that the black shaded block = difference between 2 girls’ money = $15. In other words, we know now that 1/2 block = $15. Therefore, 1 block = $30. This can be seen from the image below.
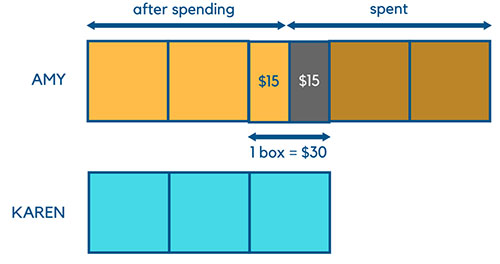
The final step is to calculate the total amount of money that both girls had in the beginning. From step one, we know there are 8 blocks in total. So the answer is 8 * $30 = $240.
3.3 Decimals
Let’s go through one last problem sum to see how to use the math model for decimals.
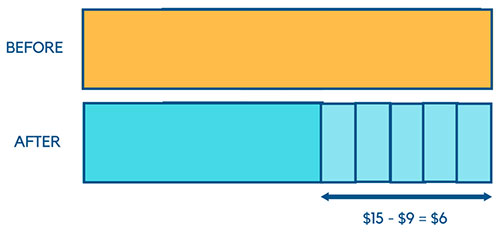
“Mary has $15 before shopping. After buying 5 identical pencil cases, she was left with $9. How much does each pencil case cost?”
The question has a before and after effect, thus making it suitable to use the change concept.

The next step is to show that the difference between the before and after can be represented by 5 blocks (to illustrate 5 pencil cases)
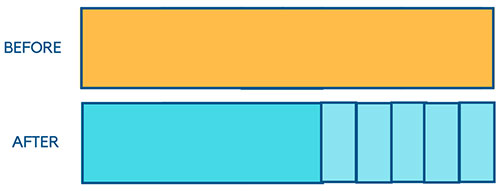
The question tells us that the 5 pencil cases are identical. Hence, to find the price of 1 pencil case, we simply have to take the difference between the before and after i.e. $15-$9 =$6 and divide that by the 5 blocks. This gives us $6/5=$1.2. This can be represented by the final math model below.
We hope this tutorial has been helpful in showing you the techniques for using the Singapore math model method. If you have further questions, please leave them in the comments.
Source: www.teach-kids-math-by-model-method.com
KooBits Math™ is The Best Way for Your Child To Learn Singapore Maths Model Method
+ Unlimited access to 100,000+ primary 1-6 maths questions
+ 1000+ maths model method video tutorials and lessons
+ Step-by-step solutions with models and diagrams
Tags: Lower Primary (7-10), mathematics, Singapore, Upper Primary (10-12)

at 8:57 PM
Great!
at 8:59 PM
It’s very useful and it taught me a lot……
at 11:59 PM
You answer to question 3.1 seems wrong. Each box should equate to 100. Total should be 1000. 600 in the morning 400 in the afternoon. 600 – 400 equals 200 extra in the morning
at 1:03 PM
Hi
Why is each box=100? It should be 40 if you looked at the steps above.
Cheers
at 9:38 PM
for my point of view, Haider is correct! each big box is equal to 200 pencils and the small boxes is equal to 100…
at 9:27 AM
Nothing wrong Haidar because if one blue square has the same value of one red square, then the 200 more will be distributed at the left five red squares (6-1=5).
at 10:33 AM
@Lina Thanks for the great response. Your explanation sounds much better than mine :)
at 10:41 PM
I agree too! It says 200 MORE in the morning and not 200 in the morning!
at 3:54 PM
@Rowena de la Cruz Hi Rowena, the above explanation (by Aaron) is correct.
Alternatively, question 3.1 can be solved using algebra.
Let the sales for the whole day be = Y
So, morning sales = 3/5 Y and afternoon sales = 1/4 * (Y-3/5 Y) = 1/10 Y
Morning sales is 200 more than Afternoon sales, mathematically it is
3/5 Y = 1/10 Y +200
Solved for Y, we will be able to get Y=400 (sales for the whole day).
So, Morning Sales = 3/5 Y = 240 and Afternoon Sales = 40.
@aaron Thanks for your explanation above, really helpful. keep it up! :)
at 10:33 AM
@AlexR Thanks!
at 8:23 PM
thank,i understand now!
at 11:29 AM
Hi Aaron,
Thanks for the sharing. It is indeed very useful. I have a nephew who has dyslexia and I can see he has great difficulties in mathematics. He will be in primary 5 next year. Does Koobits has any programs or methods that can help dyslexia students in learning mathematics?
at 5:05 PM
Hi Soon
Thanks for the comment. KooBits has a math portal called KooBits Problems Sums. It might offer your child some help :)
at 11:23 PM
They were thinking that the whole afternoon sales was the boxes that are not red. So this will make the difference one big red box. Hence, the say that the red box is 200 and the smaller unit boxes are 100 each. This is not correct of course.
at 4:37 PM
Such problems can be solvef easily by algebraic method why such elaborate & complicated method.The parents as well as the primary kids find it very tough.please give options to kids by simpler way or totally drop this model method
at 8:10 PM
This is a very interesting method. I grew up using the algebraic method, but it is good to know different approaches to teaching math. Every student is different and you have to have more than one method in your arsenal to help them. I am a tutor and one of my potential students uses this method, so I researched it and this is the first website that I found. Now I feel confident in taking the tutoring job. Thanks Aaron for the great explanation and examples above! I am going to print this page out and put it with my tutoring binder as a reference.
at 12:30 PM
I believe the solution to the example shown in 3.1 Fractions is wrong… If Peter sold 200 more pencils in the morning than in the afternoon, means 200 more are sold in the morning compared in the afternoon and not 200 are sold in the morning… Please double check!!!
at 4:02 PM
Parents The anwer given is correct. After all the cutting, morning is now 6 units and afternoon is 1 unit. The difference between them is 6-1= 5 units which then represent the 200 more pencils in morning compared to afternoon. So 1 unit = 200/5 = 40.
at 4:29 AM
how often or have ever able to use alegbraic methid to solve problem or make things happen? Singapore model can, and can be easily use to communicate with others people who didn’t even learn model before.
at 8:35 PM
And it is awesome